题意：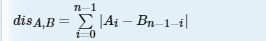

求最长的两个不相交的子序列，dis <= m ；

 

分析：

当时二分了答案，暴力匹配，TLE了，然后考虑了，O(n^2)预处理出所有区间 dis，然后答案是所有dis中>=m的最长长度吗？

不是，两个子区间可以不相邻。

 

还是二分答案，还是枚举两个区间的位置，这里已经是O(n^2)了，怎么判断他们的dis呢？ 

利用上面求出的任意两个区间的dis O(1)求出这两个子区间的dis，dis = d[i][j+mid-1] - d[i+mid][j-1]；

 

int 的二维开不了！

 

字符串细节很多！！！

#include
      
       using namespace std;const int maxn = 5005;char str[5005];unsigned short d[maxn][maxn];int len, m;bool judge(int mid){    for(int i=1; i<=len; i++)    {        if(i+mid*2-1>len) break;        for(int j= i + mid; j<=len; j++)        {            if(j+mid-1>len) break;            if(d[i][j+mid-1]-d[i+mid][j-1]<=m)                return true;        }    }    return false;}int main(){    int t;    scanf("%d", &t);    while(t--)    {        scanf("%d", &m);        scanf("%s", str+1);        len = strlen(str+1);        for(int i=0; i<=len; i++)            d[i][i] = 0;        for(int k=1; k<=len; k++)        {            for(int i=1; i<=len; i++)            {                int j = i + k - 1;                if(j>len) break;                if(j-i==1) d[i][j] = abs(str[i]-str[j]);                else d[i][j] = d[i+1][j-1] + abs(str[i]-str[j]);            }        }        int left = 1,right=len/2,ans=-1;        while(left <=right)        {            int mid = (left + right) / 2;            if(judge(mid))            {                ans = mid;                left = mid + 1;            }            else                right = mid - 1;        }        if(ans==-1)            ans = 0;        printf("%d\n", ans);    }    return 0;}